The physical world of measurement is a vast and intricate domain that plays a crucial role in our understanding of the universe. Measurement is the process of quantifying various aspects of the physical world to gain insights into its fundamental properties. It encompasses a wide range of disciplines, including physics, chemistry, biology, engineering, and many others.

Fundamentals of Measurement:

1. Units and Standards:
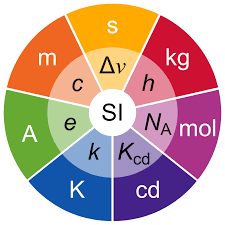
   • Measurement relies on standardized units to ensure consistency and comparability. The International System of Units (SI) is the globally accepted system that defines seven base units, including the meter (length), kilogram (mass), second (time), ampere (electric current), kelvin (temperature), mole (amount of substance), and candela (luminous intensity).
   • Reference standards, such as platinum-iridium cylinders for mass and atomic transitions for time, provide the basis for these units.
2. Precision and Accuracy:
   • Precision refers to the repeatability of measurements, while accuracy is the closeness of a measurement to the true value.
   • Instrumentation and experimental techniques are designed to minimize errors and enhance both precision and accuracy.
3. Calibration:
   • Instruments need regular calibration against known standards to ensure accuracy. Traceability to international standards is essential for maintaining the reliability of measurements.

Techniques and Instruments:

1. Metrology:
   • Metrology is the science of measurement, encompassing both theoretical and practical aspects. It includes dimensional metrology, which deals with lengths, volumes, and angles, and temporal metrology, which involves the precise measurement of time.
2. Advanced Imaging Techniques:
   • Microscopy, X-ray imaging, and scanning techniques allow scientists to visualize and measure objects at the microscopic and nanoscopic levels, providing invaluable insights into the structure and composition of matter.
3. Spectroscopy:
   • Spectroscopic techniques, such as mass spectrometry and nuclear magnetic resonance (NMR), enable the precise measurement of molecular and atomic properties, aiding in the identification and quantification of substances.
4. Particle Physics:
   • Particle accelerators and detectors are used to explore the fundamental building blocks of matter. Techniques like the Large Hadron Collider (LHC) at CERN contribute to our understanding of particle physics.

Role in Scientific Advancements:

1. Scientific Research:
   • Measurement is fundamental to scientific inquiry, allowing researchers to test hypotheses, validate theories, and discover new phenomena.
2. Technological Innovation:
   • Advances in measurement technologies drive technological innovation, leading to the development of new materials, devices, and technologies.
3. Space Exploration:
   • Precise measurements are crucial in space exploration for navigation, data collection, and the study of celestial bodies. Instruments like telescopes and spectrometers are employed to analyze distant objects.

Challenges and Future Directions:

1. Quantum Metrology:
   • Quantum technologies hold the potential to revolutionize measurement precision. Quantum metrology explores the use of quantum systems for more accurate and sensitive measurements.
2. Unified Measurement Framework:
   • Efforts are underway to establish a unified measurement framework that incorporates both classical and quantum principles, ensuring compatibility across different domains.

In conclusion, the physical world of measurement is a dynamic and evolving field that underpins scientific and technological progress. As we delve deeper into the mysteries of the universe, our ability to measure with increasing precision and accuracy becomes ever more critical.

References:

• International Bureau of Weights and Measures (BIPM). (2022). SI Brochure: The International System of Units (SI).
• Taylor, B. N., & Thompson, A. (2008). Guide for the Use of the International System of Units (SI). National Institute of Standards and Technology (NIST).
• Giacomo, P., et al. (2015). Introduction to Metrology. Machines, 3(1), 1-27.
• Arroyo-Santos, A., & Losada, J. C. (2018). Quantum metrology: An introduction to the general theory. arXiv preprint arXiv:1807.06227.

let’s delve deeper into the world of measurement, exploring key concepts and formulas that underpin the field. We’ll cover fundamental principles, units, precision, and specific measurement techniques.

1. Fundamentals of Measurement:

1.1 Units and Standards:

The International System of Units (SI) defines the following base units:

• Length (meter, m)
• Mass (kilogram, kg)
• Time (second, s)
• Electric Current (ampere, A)
• Temperature (kelvin, K)
• Amount of Substance (mole, mol)
• Luminous Intensity (candela, cd)

1.2 Precision and Accuracy:

Precision (P): P=Number of Correct DigitsTotal Digits×100P=Total DigitsNumber of Correct Digits​×100

Accuracy (A): A=Measured Value – True ValueTrue Value×100A=True ValueMeasured Value – True Value​×100

2. Techniques and Instruments:

2.1 Metrology:

• Uncertainty (U): U=ErrorMeasured Value×100U=Measured ValueError​×100

2.2 Advanced Imaging Techniques:

• Resolution (R): R=Smallest Detectable FeatureMagnificationR=MagnificationSmallest Detectable Feature​

2.3 Spectroscopy:

• Wavelength (λ) – Frequency (ν) Relationship: c=λνc=λν where cc is the speed of light.
• Mass-Energy Equivalence (E=mc²): E=mc2E=mc2 where EE is energy, mm is mass, and cc is the speed of light.

3. Role in Scientific Advancements:

3.1 Scientific Research:

• Uncertainty Principle (ΔxΔp ≥ h4π4πh​):
  • Expresses the fundamental limit to the precision of simultaneous measurements of position (ΔxΔx) and momentum (ΔpΔp) of a particle.

3.2 Technological Innovation:

• Fourier Transform: F(k)=∫−∞∞f(x) e−2πikx dxF(k)=∫−∞∞​f(x)e−2πikxdx
  • Fundamental in signal processing and the analysis of waveforms.

3.3 Space Exploration:

• Hubble’s Law: v=H0⋅dv=H0​⋅d
  • Describes the relationship between the recessional velocity (vv) of a galaxy, the Hubble constant (H0H0​), and its distance (dd).

4. Challenges and Future Directions:

4.1 Quantum Metrology:

• Quantum Uncertainty Principle: Δx⋅Δp≥ℏ2Δx⋅Δp≥2ℏ​
  • Extends the classical uncertainty principle to quantum systems.

4.2 Unified Measurement Framework:

• Quantum Mechanics Principles:
  • Incorporating principles such as superposition and entanglement into measurement frameworks.

In conclusion, the physical world of measurement involves a rich interplay of mathematical relationships and principles. From the foundational units of the SI system to the intricacies of quantum mechanics, these formulas and concepts guide our understanding of the universe at various scales.

References:

• Taylor, B. N., & Thompson, A. (2008). Guide for the Use of the International System of Units (SI). National Institute of Standards and Technology (NIST).
• Giacomo, P., et al. (2015). Introduction to Metrology. Machines, 3(1), 1-27.
• Arroyo-Santos, A., & Losada, J. C. (2018). Quantum metrology: An introduction to the general theory. arXiv preprint arXiv:1807.06227.
• Griffiths, D. J. (2005). Introduction to Quantum Mechanics. Pearson Education.