Algebra - studybuddyshareline

Basic Mathematics

About Lesson

Algebra is a fundamental branch of mathematics that deals with symbols, variables, and the rules for manipulating them. It encompasses various topics such as equations, inequalities, polynomials, functions, and more. Below is an extensive explanation of algebra along with derived formulas:

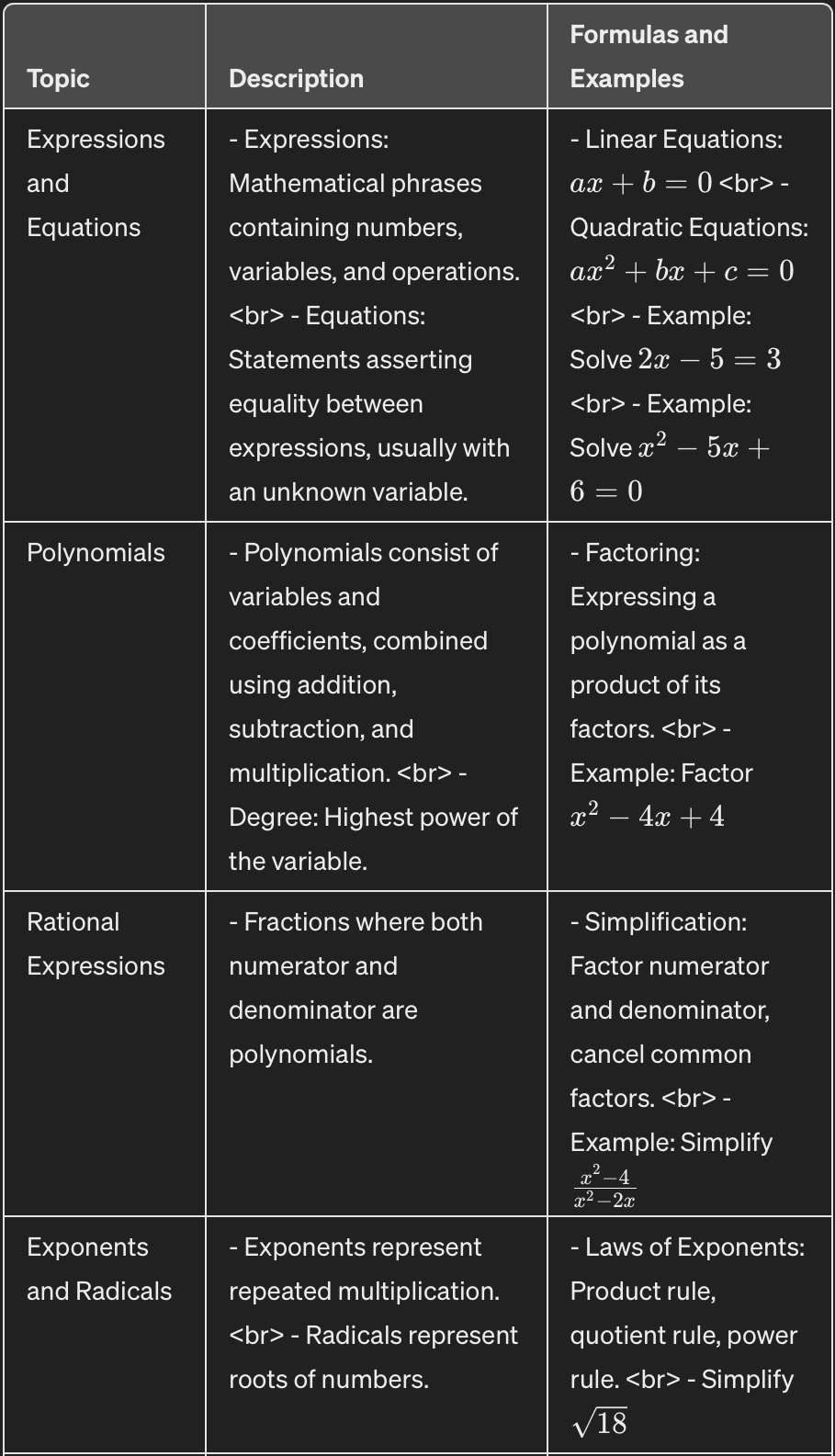
1. Expressions and Equations:

Expressions: An expression is a mathematical phrase that can contain numbers, variables, and operations like addition, subtraction, multiplication, and division. Example: $3 x + 2$ .
Equations: An equation is a statement asserting the equality of two expressions. It typically contains an unknown variable and aims to find its value. Example: $2 x - 5 = 3$ .

2. Linear Equations:

A linear equation is an equation of the form $a x + b = 0$ , where $a$ and $b$ are constants, and $x$ is the variable.
Solving a linear equation involves isolating the variable $x$ to find its value. Example: $3 x + 4 = 10$ .

3. Quadratic Equations:

A quadratic equation is a second-degree polynomial equation of the form $a x^{2} + b x + c = 0$ , where $a \neq = 0$ .
The solutions to a quadratic equation can be found using the quadratic formula: $x = 2 a - b \pm b ^{2} - 4 a c$
Discriminant ( $D$ ) of a quadratic equation ( $a x^{2} + b x + c = 0$ ): $D = b^{2} - 4 a c$
- If $D > 0$ , two distinct real roots.
- If $D = 0$ , one real root (repeated).
- If $D < 0$ , two complex roots.
Example: Solve $x^{2} - 5 x + 6 = 0$ .

4. Polynomials:

A polynomial is an expression consisting of variables and coefficients, combined using addition, subtraction, and multiplication, but not division by a variable.
Degree of a polynomial: The highest power of the variable in the polynomial.
Types of polynomials: Linear, quadratic, cubic, etc.

5. Factoring:

Factoring is the process of expressing a polynomial as a product of its factors.
Common factoring techniques: GCF (Greatest Common Factor), grouping, difference of squares, sum/difference of cubes.
Example: Factor $x^{2} - 4 x + 4$ .

6. Rational Expressions:

A rational expression is a fraction where both the numerator and denominator are polynomials.
To simplify rational expressions, factor numerator and denominator, cancel common factors if possible, and express in simplified form.
Example: Simplify $x ^{2} - 2 x x ^{2} - 4$ .

7. Exponents and Radicals:

Exponents represent repeated multiplication. Laws of exponents include product rule, quotient rule, power rule, etc.
Radicals represent roots of numbers. Properties include adding/subtracting radicals, multiplying/dividing radicals, rationalizing denominators.
Example: Simplify $18$ .

8. Functions:

A function is a rule that assigns each element of a set to exactly one element of another set.
Functions can be represented algebraically, graphically, or verbally.
Notation: $f (x)$ denotes the value of the function $f$ at $x$ .
Example: $f (x) = 2 x^{2} + 3 x - 5$ .

9. Inequalities:

An inequality is a mathematical sentence that compares expressions using inequality symbols (<, ≤, >, ≥).
Solving inequalities involves finding the range of values that satisfy the given condition.
Example: Solve $3 x - 7 < 5$ .

10. Logarithms and Exponents:

Logarithms are the inverse operations of exponentiation. The logarithm of a number to a given base is the exponent to which the base must be raised to produce that number.
Laws of logarithms: Product rule, quotient rule, power rule, change of base formula.
Example: Solve $2^{x} = 8$ .

11. Sequences and Series:

A sequence is an ordered list of numbers, while a series is the sum of the terms of a sequence.
Arithmetic sequence: Each term differs from the previous one by a constant value (common difference).
Geometric sequence: Each term is obtained by multiplying the previous one by a constant value (common ratio).
Example: Find the sum of the first 10 terms of the arithmetic sequence $2, 5, 8, 11, \dots$ .

12. Matrices and Determinants:

A matrix is a rectangular array of numbers arranged in rows and columns.
Operations on matrices include addition, subtraction, scalar multiplication, and matrix multiplication.
A determinant is a scalar value derived from the elements of a square matrix. It is used to solve systems of linear equations and calculate areas/volumes.
Example: Find the determinant of $[3257]$ .

Understanding these algebraic concepts and formulas is essential for solving complex mathematical problems encountered in competitive exams and real-world applications. Regular practice, application, and exploration of various problem-solving techniques can help students build a strong foundation in algebra and excel in their academic pursuits.